以下為協同產品設計實習 2017 Spring 期中考週的四個實習查驗題目. 完成後, 請各組員依照指示完成期中自評與互評.
(一) Fossil Server 實習查驗
本實習查驗題目必須在期中考當天 0810-0900 時段中完成.
請各組利用電腦輔助設計室中的電腦, 重新建立一台以 https 為連結協定的 Fossil Server (起始 Timeline 必須為期中考當天日期與時間為準), 並以"[a or b]g[1 ~8] 期中報告" (例如: 甲班第1組為 ag1 期中報告, 依此類推) 為 server 標題, 每一組員以學號為帳號, 各組員分別在 Wiki 中以 [學號] 期中學習心得" (例如: 4012345 期中學習心得) 為 Wiki 頁面標題, 概述上課至今的心得與自評成績.
完成後, 請報上各組 Serve 的 ip 位址進行查驗.
(二) 四連桿機構協同 Trace Point 查驗
本實習查驗題目必須在期中考當天 0910-1000 時段中完成.
請參考 電腦輔助設計實習第十週上課內容, 在各組網誌中, 以子模組 (Github Submodule) 的設定, 擷取各組員倉儲中的 T 點軌跡座標檔 (請以 midterm1.csv, midterm2.csv .... 依序命名) 後進行網際協同繪圖.
各組組員請依學號遞增排序, 排序第1者負責分析 Length=50 的 T 點軌跡圖, 其餘組員則依序將 Length -5, 分別在各組網誌中列出所有組員所完成的四連桿 T 點運動軌跡圖. (例如: 第2位組員負責 Length=45 的四連桿分析, 第3位則負責 Length=40 ....)
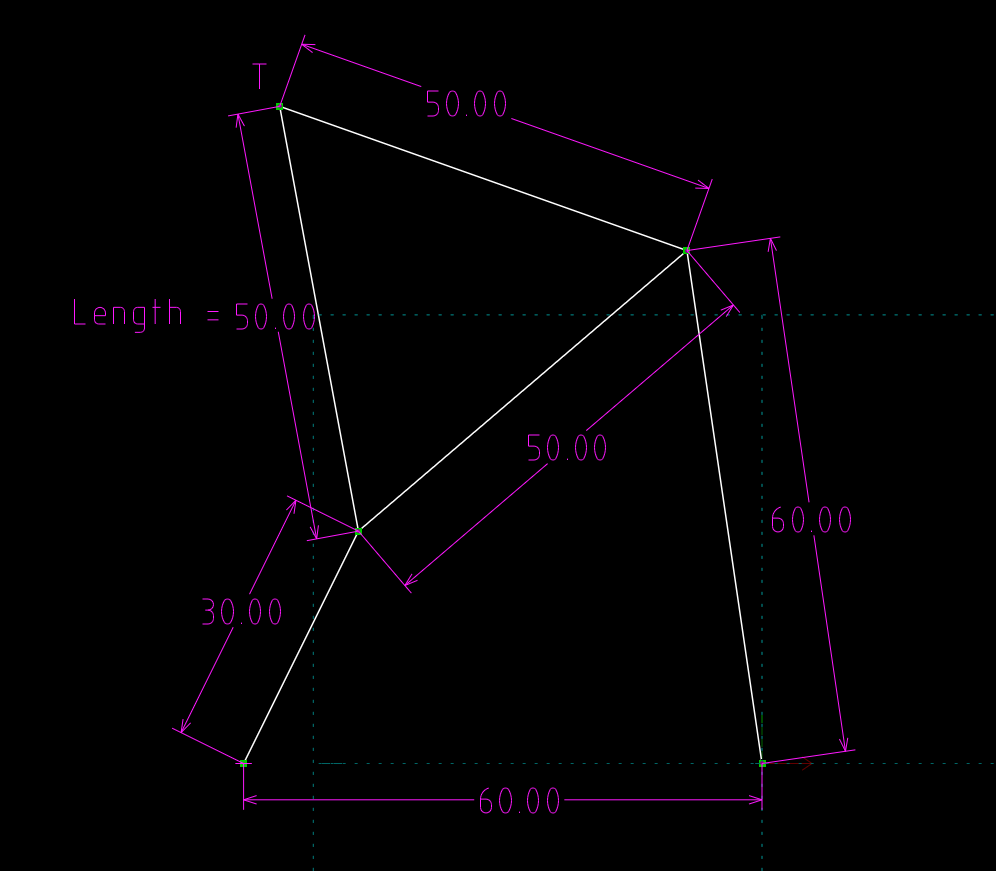
(長 30 mm 的連桿為馬達輸入桿, Trace Point 為 T 點)
參考的網際程式如下:
(三) Fourbar Walker OnShape 零件協同繪圖與組立查驗
本實習查驗題目必須在期中考當天 1010-1100 時段中完成.
請各組依照下列基本尺寸規劃, 以協同方式在 OnShape 環境中完成四連桿四足行走機構, 並分別拍攝協同規劃與實際操作影片, 將影片送到 1) Youtube 2) Vimeo 以及各組的 Fossil Server.
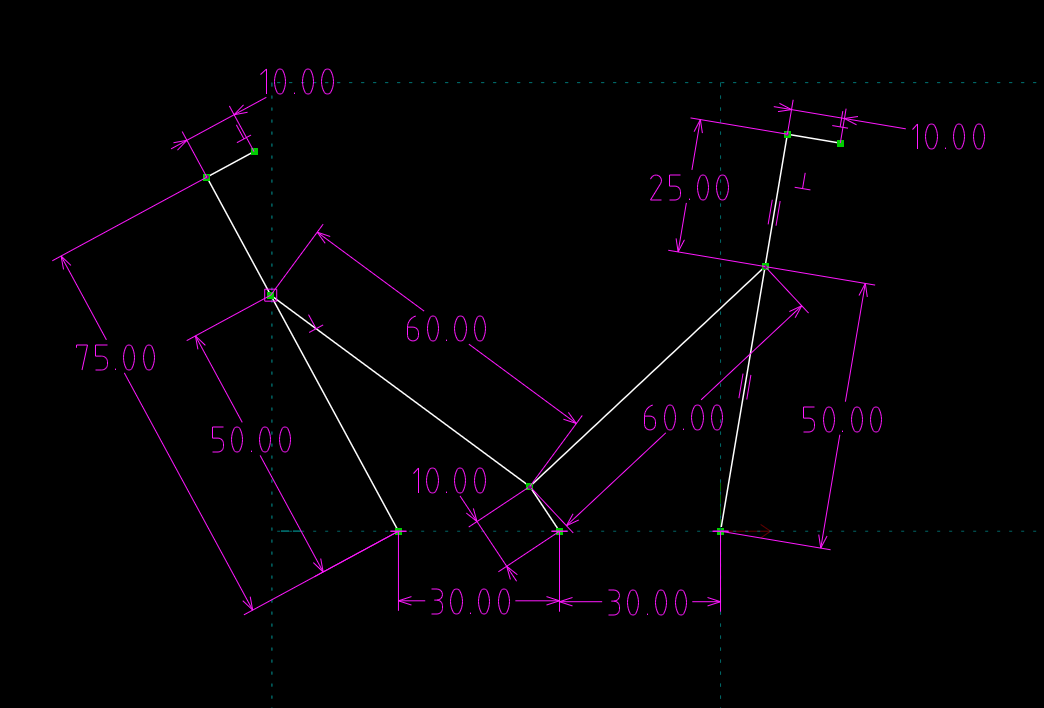
機械設計工程系-協同產品設計實習課程: 期中四連桿四足行走機構題目 from 虎尾科大機械設計工程 on Vimeo.
(四) 分組協同零件展示
本實習查驗題目必須在期中考當天 1110-1145 時段中完成, 1145-1200 將以所指定的 Ethercalc 即時表單, 取各學員的期中自評成績.
請各組於完成四足行走機構後, 轉為 STL 格式, 利用下列 viewer, 將機構展示在各組的網誌中.
利用 Madeleine 程式庫, 擷取位於 ./../data/spikeball.stl 位置的零件 stl 格式檔案:
參考用 fourbar.py:
from math import pi, cos, sin, sqrt, acos
radian = 180/pi
degree = pi/180
#PLAP
def plap(ax, ay, ac, bac, bx, by, pos):
if pos == 0:
cx= ac*cos(bac - acos((ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 + abs(ax - bx)**2 - abs(ay - by)**2)/(2*sqrt(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2)*abs(ax - bx)))) + ax
cy= ac*sin(bac - acos((ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 + abs(ax - bx)**2 - abs(ay - by)**2)/(2*sqrt(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2)*abs(ax - bx)))) + ay
else:
cx= ac*cos(bac + acos((ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 + abs(ax - bx)**2 - abs(ay - by)**2)/(2*sqrt(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2)*abs(ax - bx)))) + ax
cy= ac*sin(bac + acos((ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 + abs(ax - bx)**2 - abs(ay - by)**2)/(2*sqrt(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2)*abs(ax - bx)))) + ay
return cx, cy
#PLLP
def pllp(ax, ay, ac, cb, bx, by, pos):
if pos == 0:
cx = -((ay - by)*(-ac**2*ay + ac**2*by + ax**2*ay + ax**2*by - 2*ax*ay*bx - 2*ax*bx*by + ay**3 - ay**2*by + ay*bx**2 - ay*by**2 + ay*cb**2 + bx**2*by + by**3 - by*cb**2 - sqrt((-ac**2 + 2*ac*cb + ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 - cb**2)*(ac**2 + 2*ac*cb - ax**2 + 2*ax*bx - ay**2 + 2*ay*by - bx**2 - by**2 + cb**2))*(ax - bx)) + (ac**2 - ax**2 - ay**2 + bx**2 + by**2 - cb**2)*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))/(2*(ax - bx)*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))
cy = (-ac**2*ay + ac**2*by + ax**2*ay + ax**2*by - 2*ax*ay*bx - 2*ax*bx*by + ay**3 - ay**2*by + ay*bx**2 - ay*by**2 + ay*cb**2 + bx**2*by + by**3 - by*cb**2 + sqrt((-ac**2 + 2*ac*cb + ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 - cb**2)*(ac**2 + 2*ac*cb - ax**2 + 2*ax*bx - ay**2 + 2*ay*by - bx**2 - by**2 + cb**2))*(-ax + bx))/(2*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))
else:
cx = -((ay - by)*(-ac**2*ay + ac**2*by + ax**2*ay + ax**2*by - 2*ax*ay*bx - 2*ax*bx*by + ay**3 - ay**2*by + ay*bx**2 - ay*by**2 + ay*cb**2 + bx**2*by + by**3 - by*cb**2 + sqrt((-ac**2 + 2*ac*cb + ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 - cb**2)*(ac**2 + 2*ac*cb - ax**2 + 2*ax*bx - ay**2 + 2*ay*by - bx**2 - by**2 + cb**2))*(ax - bx)) + (ac**2 - ax**2 - ay**2 + bx**2 + by**2 - cb**2)*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))/(2*(ax - bx)*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))
cy = (-ac**2*ay + ac**2*by + ax**2*ay + ax**2*by - 2*ax*ay*bx - 2*ax*bx*by + ay**3 - ay**2*by + ay*bx**2 - ay*by**2 + ay*cb**2 + bx**2*by + by**3 - by*cb**2 + sqrt((-ac**2 + 2*ac*cb + ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2 - cb**2)*(ac**2 + 2*ac*cb - ax**2 + 2*ax*bx - ay**2 + 2*ay*by - bx**2 - by**2 + cb**2))*(ax - bx))/(2*(ax**2 - 2*ax*bx + ay**2 - 2*ay*by + bx**2 + by**2))
return cx, cy
class fourbar(object):
'''
(ax, ay) motor coord
(bx, by) rocker base coord
bac motor angle
ac link1 length
cd link2 length
db link3 length
ce triangle side1
ed triangle side2
'''
def __init__(self, ax, ay, bx, by, bac, ac, cd, db, ce, ed):
self.ax = ax
self.ay = ay
self.bx = bx
self.by = by
self.bac = bac
self.ac = ac
self.cd = cd
self.db = db
self.ce = ce
self.ed = ed
@property
def cx(self):
return plap(self.ax, self.ay, self.ac, self.bac, self.bx, self.by, pos=0)[0]
@property
def cy(self):
return plap(self.ax, self.ay, self.ac, self.bac, self.bx, self.by, pos=0)[1]
@property
def dx(self):
return pllp(self.cx, self.cy, self.cd, self.db, self.bx, self.by, pos=0)[0]
@property
def dy(self):
return pllp(self.cx, self.cy, self.cd, self.db, self.bx, self.by, pos=0)[1]
@property
def ex(self):
return pllp(self.cx, self.cy, self.ce, self.ed, self.dx, self.dy, pos=0)[0]
@property
def ey(self):
return pllp(self.cx, self.cy, self.ce, self.ed, self.dx, self.dy, pos=0)[1]
'''
# 利用 fourbar 物件建立案例
f = fourbar(ax = -60, ay = 0, bx = 0, by = 0, bac = 50*degree, ac = 30, cd = 50, db = 60, ce = 50, ed = 50)
# 利用 fourbar 物件案例的方法求各點座標
#f.cx, f.cy 為 C 點座標
#f.dx, f.dy 為 D 點座標
#f.ex, f.ey 為 E 點座標
'''
Brython 四連桿 E 點運動軌跡繪圖程式: